tenflow.js--三种方法用js搭建神经网络实现曲线拟合

引言

这一段时间研究生生涯已经走进了尾声，也一直忙于论文没有关注前端方面的工作。偶然的机会，在知乎上看到了一篇文章前端人工智能？TensorFlow.js 学会游戏通关。我的内心是很激动的，终于，也能在前端直接搭神经网络，跑分类了。不过该文章，对于tensorflowjs的介绍太少，直观的游戏ai应用确实很好，但是对于初次接触的人，还是从最基础的框架使用开始更好，于是就有了这篇文章。本文抛开了复杂的实际问题，选择曲线拟合这个最简单易懂的情景，使用3种逐步深入的方法来完成目标问题的解决。从最基础的数学方法，到借助底层api构建神经网络，再到最终借助高层次api构建神经网络，一步步熟悉框架的使用，希望能够帮助后来者快速上手。 demo地址(目测手机版后面两个方法训练不出来，建议pc版访问)

目标问题介绍

本文的目标是实现曲线拟合。直观上，曲线可看成空间质点运动的轨迹，用数学表达式来就是y=f(x)，举个例子，y=x,y=x^2+5……等等，就是曲线。而曲线拟合，用简单的话来说，就是知道一条曲线的某些点，来预测要 y=f(x) 的表达式是什么。如下图：

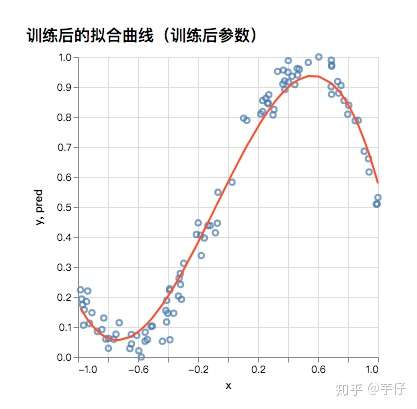
图中，蓝色点点就是已知曲线中的某些点（本例中数目为100），红色曲线就是拟合出的结果，也就是本文要实现的曲线拟合。

工具，环境说明

用到的前端相关的库有：

1. tensorflow.js，用来搭建神经网络，训练等。tensorflow的文档写的很好，第一篇讲了核心概念，第二篇就讲到了如何拟合一条曲线，不过它只使用了线性模型的方法进行拟合，没有通过神经网络，这也是本文存在的理由，笔者在看了该文档之后，一方面，将文档中提到的方法采用面向对象的方法重构，另一方面，通过学习其api，搭建神经网络来实现相同的功能。
2. vega-embed，这个就是用来绘制曲线和散点的工具，用escharts等可视化工具也行，这里不是关键。

另外由于在代码中使用了class，async等等es6,es7的用法，故在实际使用的时候需要用到babel。本文使用的打包工具是parcel，号称是零配置的 Web 应用程序打包器，体验了一下，确实好用。

源码放在了github上，使用说明见README.md。demo更加直观。

样本点数产生方法

在这个问题中，首先需要产生样点。本文设定曲线方程为 y = ax^3 + bx^2 + c*x + d，首先随机产生100个x值，再带入方程计算y值。最终产生本文的测试样点，核心代码如下：其中涉及到一些tensorflow的api，会穿插在注释中简单介绍。

//导入tensorflow
import * as tf from '@tensorflow/tfjs';
/*
    *输入参数：
    *num：样点数目
    *coeff：参数对象{a: , b: , c: , d:  };
    *sigma：样点偏移原曲线范围
    *输出参数：
    {
    x: 样点横坐标值
    y: 样点纵坐标值
    }
*/
export function generateData(num, coeff, sigma = 0.04) {
    //将代码用tf.tidy包裹，可以清除执行过程中的tensor变量
    return tf.tidy(() => {
        //tf.scalar: 产生一个tensor变量，其值为输入的参数
        const [a, b, c, d] = [
            tf.scalar(coeff.a), tf.scalar(coeff.b), tf.scalar(coeff.c),
            tf.scalar(coeff.d)
        ]
        //tf.randomUniform([num],-1,1): 产生-1,1之间的均匀分布的值组成的[num]    
        //矩阵,此处就是1*100的矩阵, [2,3]表示2*3的矩阵(二维数组)
        const x = tf.randomUniform([num], -1, 1);
        //计算a*x^3 + b*x^2 + c*x + d+(0~sigma之间服从正太分布的随机值)
        const y = a.mul(x.pow(tf.scalar(3)))
            .add(b.mul(x.square()))
            .add(c.mul(x))
            .add(d)
            .add(tf.randomNormal([num], 0, sigma));
        //对输出值进行归一化
        const ymin = y.min();
        const ymax = y.max();
        const yrange = ymax.sub(ymin);
        const yNormalized = y.sub(ymin).div(yrange);

        return {
            x,
            yNormalized
        };
    })
}

其中，api仅仅介绍了当前情景的功能，其还有一些可选参数没有进行介绍，具体可以查看官方文档，基本上看名字能猜出大概，结合官方文档不难理解，此处不再过多介绍。

从上述代码可以看出，TensorFlow 提供了很好的api，包括服从均匀分布，正态分布参数的产生，tensor类型带来的矩阵加减乘除运算，最大最小值计算等功能，以及自带的缓存清理函数tidy。这些方法构成了整个运算的基础，大大方便了使用者。

这一小节中，通过上述代码，产生num个x，y，构成了本文所述的样本点，为后文曲线拟合做好了样本准备。后续将借助TensorFlow 通过3种不同方法实现对该曲线的拟合。

线性模型方法实现曲线拟合

首先介绍第一种方法，也就是tensorflow文档第二篇中提到的方法—构建线性模型进行拟合。这个方法需要有一个已知条件，即已经知道预测的模型为 y = a*x^3 + b*x^2 + c*x + d。
知道算法模型之后，原理如下：

1. 初始化a,b,c,d，取随机值即可
2. 根据随机的参数a,b,c,d按照模型 y = a*x^3 + b*x^2 + c*x + d对100个点进行计算，根据得到的结果，采取一定的手段（原理是偏导，但是这里不需要自己计算，tensorflow会解决这里的调整问题）调整a,b,c,d。使计算出来的y与原来的y差值最小。
3. 经过多次步骤二，y与原本的y值差值足够小，就可以认为a,b,c,d就是要求的最终参数。此时，根据该曲线计算出结果并绘制出来，就实现了曲线的拟合。

将上述过程进行抽象，可以得到以下几个过程：

1. predict(inputXs)，根据已知的样点，计算该样点对应的y值
2. loss(predectedYs,inputYs)，计算y与输入的y的差值
3. train(inputXs,inputYs)，进行一次训练，通过调整参数来使得loss更小
4. fit(inputXs,inputYs，iterations)，进行曲线拟合，多次调用train来完成训练

根据上述方法，构建了一个简单的线性模型类，代码如下：

import {Model} from './model';
import * as tf from '@tensorflow/tfjs';

function random(){
    return (Math.random()-0.5)*2;
}

export class Linear_Model extends Model{
    constructor(){
        super();
        this.init();
    }
    init(){
        this.weights = [];
        this.weights[0] = tf.variable(tf.scalar(random()));//对应参数a
        this.weights[1] = tf.variable(tf.scalar(random()));//对应参数b
        this.weights[2] = tf.variable(tf.scalar(random()));//对应参数c
        this.bias = tf.variable(tf.scalar(random()));//对应参数d

        this.learningRate = 0.5;
        //设置优化器，自动调整参数
        this.optimizer = tf.train.sgd(0.5);
    }
    //根据输入样点计算输出
    predict(inputXs){
        return tf.tidy(()=>{
            //y = weight[0]*x^3+weight[1]*x^2+weight[2]*x+biases
            return this.weights[0].mul(inputXs.pow(tf.scalar(3)))
                .add(this.weights[1].mul(inputXs.square()))
                .add(this.weights[2].mul(inputXs))
                .add(this.bias);
        })
    }
    train(inputXs,inputYs){
        //通过优化器的minimize方法来实现对参数的减少
        this.optimizer.minimize(()=>{
            //根据输入预测输出
            const predictedYs = this.predict(inputXs);
            //计算预测输出与原本的输出差值
            return this.loss(predictedYs,inputYs);
        })
    }
    //计算差值，此处采用均方误差，就是差值平方再取平均值
    loss(predictedYs,inputYs){
        return predictedYs.sub(inputYs).square().mean();
    }
    //多次调用train来调整参数
    fit(inputXs,inputYs,iterationCount = 100){
        for(let i = 0;i<iterationCount;i++){
            this.train(inputXs,inputYs);
        }
    }
}

在上述代码中，用到了tensorflow的tf.train.sgd();方法，这个方法定义了一个优化器，就是通过调整参数来实现loss的不断降低，sgn是梯度下降法，类似的还有adam等。其优化的变量涉及到了inputXs,inputYs,weights(对应之前说的a,b,c,d)，那么它是如何判断哪些参数可以调整，哪些不能调整的呢？答案是tf.variable，在优化器优化的过程中，只能调整涉及到的通过tf.variable定义过的变量，在这个例子中，就只有this.weights。当执行train方法的时候，优化器会根据loss的计算过程，调整variable参数，使得loss往小的方向去走（严格来讲，不一定，和学习率等很多因素有关，但是这里问题比较简单，故不讨论，感兴趣可以看看coursera上吴恩达的机器学习课程）。经过多次train之后，就可以得到合适的参数，此时loss只要足够低，那么使用这些参数得到的结果就与愿结果无限趋近，可以认为实现了曲线的拟合。

最终调用代码如下：

import {
    Linear_Model
} from './linear_model';
import {
    generateData
} from './data';
import {
    plotData,
    plotCoeff,
    plotDataAndPredictions
} from './ui'
import * as tf from '@tensorflow/tfjs';

async function liner_method() {
    //新建线性预测模型  
    const linear_model = new Linear_Model();

    const trueCoefficients = {
        a: -.8,
        b: -.2,
        c: .9,
        d: .5
    };
    //调用数据产生函数，产生测试样本
    const trainingData = generateData(100, trueCoefficients);
    //调用ui层的方法进行样点的绘制，此处ui层不做详细介绍
    await plotData('#data .plot', trainingData.x, trainingData.yNormalized);
    //先做一次预测，看看初始参数拟合的曲线形状
    const predictionsBefore = linear_model.predict(trainingData.x);
    //绘制样点和曲线
    await plotDataAndPredictions('#random .plot', trainingData.x, trainingData.yNormalized, predictionsBefore);
    //调用fit方法进行训练
    linear_model.fit(trainingData.x, trainingData.yNormalized);
    //再次计算曲线，此时参数已经经过训练
    const predictionsAfter = linear_model.predict(trainingData.x);
    //绘制曲线
    await plotDataAndPredictions('#trained .plot', trainingData.x, trainingData.yNormalized, predictionsAfter);
}

上述代码就是对本文定义的Linear_Model的一个使用方法，最终完成了曲线拟合这个目标。

这种方法的训练速度快，但是缺点在于需要事先知道模型形状(y = ax^3 + bx^2 + c*x + d)，不然不好进行预测。到这里，其实还没有涉及到神经网络的使用，但是所谓神经网络本质上也是参数的不断调整，只是更加复杂一些。加下来将使用底层api构建一个包含一层隐含层的神经网络来解决这个问题。不需要事先知道模型形状也能完成曲线的拟合。

底层api构建神经网络实现曲线拟合

神经网络的原理这里就不介绍了，感兴趣可以看coursera上吴恩达或者ufldl的介绍，都比较详细。
在这个问题中，由于是线性函数，所以拟合起来并不困难，这里采取1-6-1的结构，第一个1是输入层，这里是一维，所以输入层为1，隐含层选择6，这里其实5，4，7都可以，只是需要训练的次数不同而已。最后一层输出层为1，因为输出就是y值，也是一维的。

按照上一节抽象出来的过程，也需要手动实现predict，loss等函数。神经网络，与上述不同的地方就在与参数的构建，predict计算方式不同，其它地方其实基本一样。代码如下：

import {
    Model
} from './model';
import * as tf from '@tensorflow/tfjs';
export default class NNModel extends Model {
    constructor({
        inputSize = 3,
        hiddenLayerSize = inputSize * 2,
        outputSize = 2,
        learningRate = 0.1
    } = {}) {
        super();
        //定义隐藏层，输入层，输出层，优化器函数
        this.hiddenLayerSize = hiddenLayerSize;
        this.inputSize = inputSize;
        this.outputSize = outputSize;
        this.optimizer = tf.train.adam(learningRate);
        this.init();
    }
    //初始化神经网络参数
    init() {
        this.weights = [];
        this.biases = [];
        //第一层参数为1*6的矩阵
        this.weights[0] = tf.variable(
            tf.randomNormal([this.inputSize, this.hiddenLayerSize])
        );
        //第一层偏置
        this.biases[0] = tf.variable(tf.scalar(Math.random()));
        // Output layer
        //第二层参数为6*1的矩阵
        this.weights[1] = tf.variable(
            tf.randomNormal([this.hiddenLayerSize, this.outputSize])
        );
        this.biases[1] = tf.variable(tf.scalar(Math.random()));
    }
    //预测函数，激活函数选择sigmoid，matMux表示矩阵乘法
    predict(inputXs) {
        const x = tensor(inputXs);
        return tf.tidy(()=>{
            const hiddenLayer = tf.sigmoid(x.matMul(this.weights[0]).add(this.biases[0]));
            const outputLayer = tf.sigmoid(hiddenLayer.matMul(this.weights[1]).add(this.biases[1]));
            return outputLayer;
        })
    }
    train(inputXs,inputYs){
        this.optimizer.minimize(()=>{
            const predictedYs = this.predict(inputXs);
            return  this.loss(predictedYs,inputYs);
        })
    }
    loss(predictedYs, inputYs) {
        const meanSquareError = predictedYs
          .sub(tensor(inputYs))
          .square()
          .mean();
        return meanSquareError;
      }
}

上述代码中，涉及到了sigmoid函数，也就是神经网络的激活函数，很基础的概念，不多介绍。另外一个就是matMux，相当于矩阵乘法。

在实际使用时，方法和线性模型几乎一致，此处不贴代码，最终需要进行500多次的训练，才能达到和上述线性模型同样的效果。但是在不知道模型的情况下，还能拟合该曲线，这就是神经网络方法最大的优势。不需要人为构建模型，也能解决问题。

但是上述的写法存在一个问题，就是现在是1个隐含层，计算可以通过predict中两三行的代码搞定，但是层数多了之后，手动的一次次编写中间代码，实在也是一个体力活，而且容易出错。为了解决这个问题，tensorflow提供了一种更高层次的构建方法，就是下一节要介绍的方法。

高层次api构建神经网络

在tensorflow中，有一个高层次的api，tf.sequential()，其用法直接通过实例来解释：

const model = tf.sequential();
model.add(tf.layers.dense({
    units: 6,
    inputShape: [1],
    activation:'sigmoid'
}));
model.add(tf.layers.dense({
    units:1,
    activation:'sigmoid'
}));
model.compile({
    optimizer:tf.train.adam(0.1),
    loss:'meanSquaredError'
})

通过上述的代码，就构建了一个神经网络，该网络有3层，一个是输入层，1维，隐藏层，6维，最后输出层，1维。上述代码中，model.add了两次，这是因为输入层其实就是输入样本，不需要计算，所以不需要添加，只需要在后续层添加的时候指定inputShape即可。其中，activation就是激活函数，这里直接选择signoid，而compile，就是完成模型的构建，需要指定优化器和loss计算方法（可以用字符串也可以传入一个自定义计算的函数）。此时，就完成了一个神经网络的搭建。用法如下：

//预测样本对应的值
const predictionsBefore = model.predict(trainingData_nn.x);
//绘制结果
await plotDataAndPredictions('#random3 .plot', trainingData.x, trainingData.yNormalized, predictionsBefore);
//进行训练
const h = await model.fit(trainingData_nn.x,trainingData_nn.yNormalized,{
      epochs:200,
      batchSize:100
})
//训练结束后再次计算曲线y值
const predictionsAfter = model.predict(trainingData_nn.x);
//绘制结果
await plotDataAndPredictions('#trained3 .plot', trainingData.x, trainingData.yNormalized, predictionsAfter);

可以看出，tensorflow提供的model,可以直接使用fit，predict，同时不需要手动指定weights，可以说是很方便了。

小结

本文算是对官方文档的一个深入，选择最简单的曲线拟合问题入手，从最简单的线性模型到手动搭建神经网络，再到利用高层api来搭建神经网络，解决了曲线拟合的问题。

总体来说，最好的搭建姿势还是借助高层api，可以很方便快捷的搭建想要的神经网络，十分好用。希望能让后来者少走一些弯路。当然，可能文中也会有些错误，如有发现，还请指出，谢谢🙏。